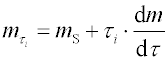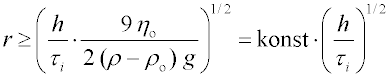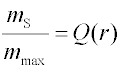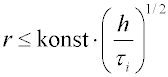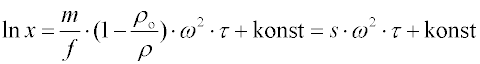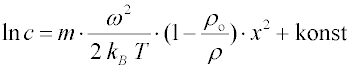sedimentační analýza
sedimentation analysis
Sedimentační rychlost v gravitačním poli
Zpracování sedimentačních dat pro
hrubé disperze je založeno na
Stokesově rovnici pro kulovité částice,
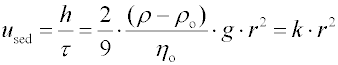
(1)
kde
h je změna výšky sloupce sedimentující disperze za dobu
τ,
k je konstanta, zahrnující rozdíl hustot sedimentující částice a disperzního prostředí
(ρ – ρo), viskozitu disperzního prostředí
ηo a tíhové zrychlení
g, a
r je poloměr kulovité částice nebo
efektivní poloměr (tj. poloměr koule z daného materiálu, která by v prostředí stejné hustoty a viskozity sedimentovala stejnou rychlostí) v případě systémů s
anizometrickými částicemi.
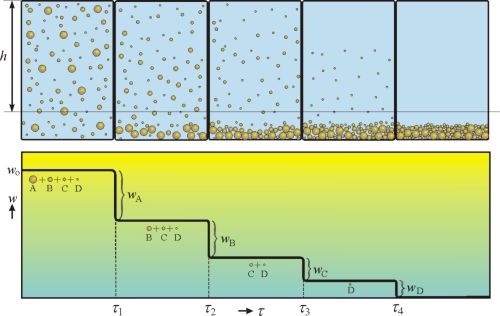
Zpracování dat získaných měřením koncentrace sedimentující disperze v závislosti na čase ve stejné hloubce. V rozmíchané disperzi je na počátku stejná koncentrace w0 ve všech místech. U monodisperzního systému padají všechny částice stejnou rychlostí; touto rychlostí se pohybuje také hranice vyčeření. V čase τ, v němž hranice vyčeření dosáhne hloubky h, poklesne koncentrace disperze na nulu a poloměr částic je dán rovnicí (1).
Obr. 1 znázorňuje časovou závislost koncentrace v sedimentujícím
paucidisperzním systému. V hloubce
h jsou zaregistrovány postupně čtyři poklesy koncentrace, které odpovídají úplné sedimentaci jednotlivých frakcí od nejhrubší po nejjemnější.
 |
|
|
Obr. 1 Časová závislost hmotnostní koncentrace w pro systém o čtyřech úzkých frakcích s poloměry rA > rB > rC > rD v koncentracích wA, wB, wC, wD
|
Poměry
wA/wo,
wB/wo,
wC/wo,
wD/wo udávají zastoupení jednotlivých frakcí, tj. hodnoty
diferenciální rozdělovací funkce F(rA),
F(rB),
F(rC),
F(rD). Pro rozměry částic platí
Pro
polydisperzní systémy je časová závislost koncentrace dána hladkou klesající křivkou. Disperzní podíl představuje velké množství frakcí o různých poloměrech, z nichž každá sedimentuje jako monodisperzní systém, nezávisle na ostatních. Celková koncentrace
w(τi) v určité hloubce
h v čase
τi je tvořena všemi dosud neusazenými frakcemi, jejichž částice jsou menší než
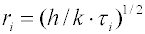
. Poměr koncentrací
w(τi)/wo tedy představuje integrální rozdělovací funkci
I(ri).
Zpracování dat získaných sledováním přírůstku hmotnosti sedimentu s časem - vyhodnocení
sedimentační křivky.
Sedimentační křivka
monodisperzní soustavy (obr. 1a) je přímková. Protože koncentrace systému je v čase
τ = 0 stejná ve všech výškách a všechny částice sedimentují konstantní rychlostí, roste hmotnost sedimentu rovnoměrně. V čase
τ1, kdy jsou všechny částice usazeny, je
m = mmax = konst, a na závislosti
m = m(τ) objeví zlom. Poloměr částic je dán rovnicí (1) (
h je hloubka, v níž je ponořena miska vah).
 |
|
|
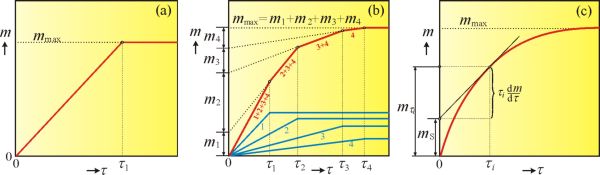
Obr. 2 Sedimentační křivka pro (a) monodisperzní, (b) paucidisperzní, (c) polydisperzní systém
|
Pro
paucidisperzní systém (obr. 2b znázorňuje systém s částicemi čtyř různých velikostí) je sedimentační křivka tvořena lomenou čarou, která je součtem sedimentačních křivek jednotlivých monodisperzních podílů. Zlomy odpovídají okamžikům ukončení sedimentace jednotlivých frakcí
τ1,
τ2,
τ3,
τ4, úseky na svislé ose hmotnostem jednotlivých frakcí
m1 až
m4.
Časová závislost hmotnosti sedimentu pro
polydisperzní systém je spojitá křivka (obr. 2c). Hmotnost sedimentu v čase
τi může být vyjádřena jako součet dvou členů:
První člen představuje hmotnost všech frakcí, které jsou v tomto okamžiku již usazeny, mS, pro jejichž poloměr r ze Stokesovy rovnice plyne
kde (ρ - ρo) je rozdíl hustot sedimentující částice a disperzního prostředí, ηo - viskozita disperzního prostředí a g je tíhové zrychlení. Poměrem
Druhý člen je roven hmotnosti částečně sedimentovaných frakcí, pro jejichž poloměr platí
Sedimentační rychlost v poli ultracentrifugy
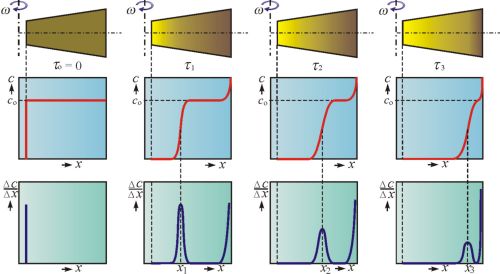
I v kyvetě ultracentrifugy se při sedimentaci vytváří oblast vyčeření. Její hranice se pohybuje v radiálním směru od osy otáčení stejnou rychlostí, jakou sedimentují disperzní částice. Na snímcích, získaných v různých časových okamžicích τ1, τ2, τ3 je odečítána poloha rozhraní (x1, x2, x3) jako souřadnice maxima gradientu koncentrace (obr. 3). Směrnice závislosti ln x na čase
(viz
sedimentační rychlost) udává
sedimentační koeficient s, který je úměrný
poměru hmotnosti částice a koeficientu tření,
m/f, (
ω je úhlová rychlost otáčení rotoru ultracentrifugy,
ρ a
ρo - hustoty disperzního podílu a disperzního prostředí). K získání informací o velikosti částic je zapotřebí znát hodnotu koeficientu tření. Ten může být např. vypočten podle
Einsteinovy rovnice ze změřeného difuzního koeficientu.
Vzhledem k interakcím mezi částicemi jsou hodnoty sedimentačního koeficientu závislé na koncentraci; s rostoucí koncentrací sedimentační koeficient obvykle klesá. Pak je třeba extrapolovat naměřená data na nulovou koncentraci. Na koncentračním rozhraní dochází k difuzi, což vede k rozplývání původně ostrého rozhraní. Šířka rozhraní závisí na velikosti difuzního koeficientu.
 |
|
|
Obr. 3 Zpracování měření sedimentační rychlosti v ultracentrifuze
|
U
polydisperzních systémů sedimentuje každá frakce jinou rychlostí a vytváří vlastní koncentrační rozhraní. Na křivce koncentračního gradientu pak buď vznikají oddělené píky, charakterizující jednotlivé frakce, liší-li se dostatečně sedimentačními koeficienty, nebo jednotlivé píky splývají. Závislost
ln x na
τ má pak tvar lomené čáry, v systémech se spojitou rozdělovací křivkou velikosti částic má tvar plynulé křivky. Z jejího průběhu je možno vyhodnotit distribuční funkci velikosti částic.
Sedimentační rovnováha v poli ultracentrifugy
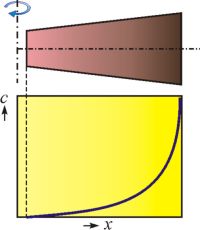
Koncentrace
disperzního podílu v kyvetě ultracentrifugy roste exponenciálně se vzdáleností od osy rotace (obr. 4).
 |
|
|
Obr. 4 Průběh koncentrace disperzního podílu v kyvetě po ustavení sedimentační rovnováhy
|
Pro
monodisperzní systémy je tato závislost přímková a z její směrnice je možno získat hodnotu hmotnosti částice
m (při rovnovážných měřeních nezávisí směrnice na koeficientu tření).
U
polydisperzních systémů představuje koncentrační profil součet exponenciálních závislostí pro jednotlivé druhy. Závislost
ln c vs.
x2 je pak lomená čára nebo častěji křivka, která se vyhodnocuje pomocí nelineární regrese. Kvantitativní charakterizace statistického rozdělení molárních hmotností vyžaduje řadu měření a složité vyhodnocovací postupy. V jednodušším případě je možno vyhodnocením získat
střední molární hmotnost (hmotnostní střed).
Grafy souvislostí do úrovně:
I  II
II 
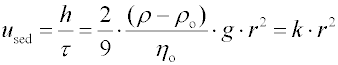 (1)
(1)
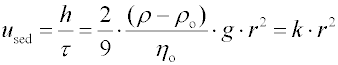 (1)
(1)

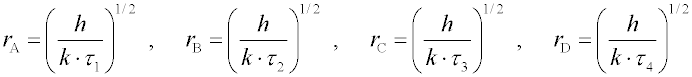
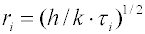 . Poměr koncentrací w(τi)/wo tedy představuje integrální rozdělovací funkci I(ri).
. Poměr koncentrací w(τi)/wo tedy představuje integrální rozdělovací funkci I(ri).