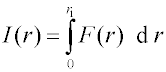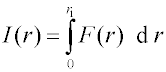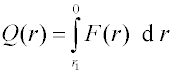I_W(r), popř. I_N(r), udává, jaký podíl hmotnosti z celkové hmotnosti, popř. počtu částic z  celkového počtu částic disperzního podílu, tvoří frakce, jejichž částice mají poloměr menší nebo stejný než určitá zvolená hodnota r₁

Q_W(r), popř. Q_N(r) - doplňková integrální rozdělovací funkce - udává, jaký podíl hmotnosti z celkové hmotnosti, popř. počtu částic z celkového počtu částic disperzního podílu, tvoří frakce, jejichž částice mají poloměr větší nebo stejný než určitá zvolená hodnota r₁:

Integrální rozdělovací funkce je tedy možno vypočítat z průběhu diferenciálních rozdělovacích funkcí analytickou nebo grafickou integrací - I(r) je dáno plochou, kterou vymezuje abscisa pro dané r₁ a levá část křivky F(r); Q(r) plochou, vymezenou abscisou pro r₁ a pravou částí křivky F(r).

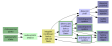
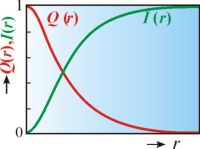
Průběh obou integrálních funkcí pro polydisperzní systém ukazuje obr. 1. Obě křivky mají inflexní bod, který odpovídá rozměru nejhojněji zastoupených částic.