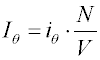|
iθ
|
je intenzita světla rozptýleného jednou částicí (molekulou) pod úhlem θ,
|
|
Io
|
celková intenzita dopadajícího (primárního) záření,
|
|
εo
|
permitivita vakua (8,85419∙10–12 C2 J–1 m–1),
|
|
α
|
polarizovatelnost částice, tj. moment dipólu indukovaného v částici elektrickým polem o jednotkové intenzitě, kterou Rayleigh vyjádřil z Clausiovy-Mossottiovy rovnice pomocí indexů lomu disperzního podílu (n) a čistého disperzního prostředí (n0),
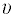 objem disperzní částice objem disperzní částice
|
|
λ
|
vlnová délka primárního i rozptýleného světla v daném disperzním prostředí (λ = λo / n0, kde λo je vlnová délka záření ve vakuu),
|
|
r
|
vzdálenost detektoru, měřícího intenzitu, od zdroje rozptýleného světla (viz měření rozptylu světla),
|
|
θ
|
úhel pozorování, tj. úhel sevřený primárním paprskem a paprskem rozptýleného světla, který dopadá do detektoru,
|
|
F(θ)
|
je funkce úhlu pozorování, jejíž tvar závisí na charakteru primárního paprsku:
-
Je-li primární paprsek vertikálně polarizovaný (intenzita elektrického pole se mění periodicky ve směru osy z), osciluje indukovaný dipól ve stejném směru. Rozptýlené světlo je také vertikálně polarizováno a šíří se ve všech směrech roviny xy se stejnou intenzitou, takže pro každé θ je
-
Pro horizontálně polarizovaný paprsek platí
-
Pro nepolarizované světlo, které je považováno za složené ze dvou komponent polarizovaných kolmo na sebe, je intenzita rozptýleného světla dána průměrnou hodnotou obou předchozích případů, takže platí
|
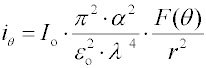
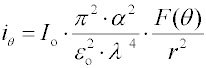
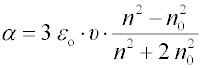
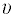 objem disperzní částice
objem disperzní částice