kde
τ je doba, za kterou částice prodifunduje do vzdálenosti
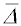
. Difuzní koeficient je možno vyjádřit z
Einsteinovy rovnice a v případě velkých kulovitých částic lze pro koeficient tření použít
Stokesovu rovnici
Platnost tohoto vztahu -
Einsteinovy-Smoluchowského rovnice (pro kulovité částice se někdy používá označení
Einsteinova-Smoluchowského-Stokesova rovnice) - byla experimentálně prokázána na základě
ultramikroskopických měření středního posuvu pro zlatý sol, na základě sledování závislosti mezi
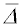
a viskozitou disperzního prostředí i sledováním teplotní závislosti středního posuvu
[
87], [
57], [
58], [
59], [
60], [
74], [
75].
Einsteinova-Smoluchowského rovnice byla také použita k výpočtu Avogadrovy konstanty.
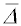 , který odvodili nezávisle na sobě Einstein
[20], [21] (1905) a Smoluchowski
[81], [82]
(1906):
, který odvodili nezávisle na sobě Einstein
[20], [21] (1905) a Smoluchowski
[81], [82]
(1906):
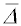 , který odvodili nezávisle na sobě Einstein
[20], [21] (1905) a Smoluchowski
[81], [82]
(1906):
, který odvodili nezávisle na sobě Einstein
[20], [21] (1905) a Smoluchowski
[81], [82]
(1906):
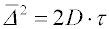
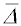 . Difuzní koeficient je možno vyjádřit z Einsteinovy rovnice a v případě velkých kulovitých částic lze pro koeficient tření použít Stokesovu rovnici
. Difuzní koeficient je možno vyjádřit z Einsteinovy rovnice a v případě velkých kulovitých částic lze pro koeficient tření použít Stokesovu rovnici
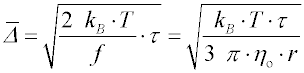
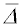 a viskozitou disperzního prostředí i sledováním teplotní závislosti středního posuvu
[87], [57], [58], [59], [60], [74], [75].
Einsteinova-Smoluchowského rovnice byla také použita k výpočtu Avogadrovy konstanty.
a viskozitou disperzního prostředí i sledováním teplotní závislosti středního posuvu
[87], [57], [58], [59], [60], [74], [75].
Einsteinova-Smoluchowského rovnice byla také použita k výpočtu Avogadrovy konstanty.